 |
バイナリーツリー(二分木) はこれまでのデータ構造とは異なり、ソートなどにおいて最初から 効率良く(つまり後で利用しやすいように)データを格納するために考案 されたものである。その構成要素は、双方向リンクドリストと同じく、 データへのポインタと、自分自身を参照する2つのポインタからなって いる。違いは、双方向リンクドリストが同じ直線上の右左へのポインタ によってつながっていたのに対して、バイナリーツリーでは木のように、 広がって行く点にある。
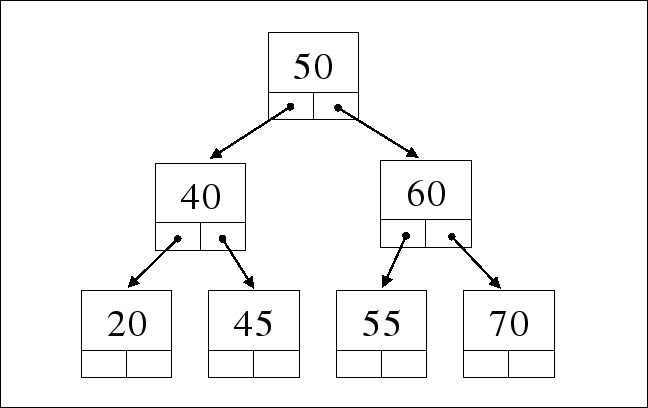
バイナリーツリーでは左側にデータを付け加えるか、右側に付け加えるか を data から導かれる値で判断をする(勿論 data 以外から決定しても良い)。 例えば、学生のテストの点数で判断をするとしよう。まず、最初のデータ は 50 点だとすると、これが最初のツリーの根っ子になる(これには右左 はない)。次にデータを登録する際に、もし40点ならば50点より小さいので、 左に登録する。次に、45点ならば、50点よりは小さいので左に行き、 そこでは 40 点が登録されているので、それよりは大きいので右に登録 する。このように点数が小さいものは左に、点数が大きいものは右に 登録するようにするのである。うまくツリーが広がるように登録されれば、 ポインタをたどる回数はリンクドリストよりは少なくなり素早い登録が 可能になり、同時にある値のデータを検索する際にも少ない検索回数で 目的の値に到達できる(リンクドリストならば必ず頭から順に検索しなけ ればならない)。更には、点数の順序に並べ変える(ソート)ような事も、 比較的に高速に行えるようになっているが、少しプログラム的には複雑に なるのでここでは取り上げない。
struct BTREE {
struct BTREE *left, *right;
int point;
};
typedef struct BTREE Btree;
static Btree *root=NULL;
|
バイナリーツリーにおいても、木の根っ子へのポインタは何らかの形で
保持していなければならない。上の例では、static に保持するように
しているが(この場合複数のバイナリーツリーを作れないという欠点も
ある)、呼び出す側のプログラムで保持する場合もあるだろう。
また、この例では格納するデータは直接 point に整数型で入れているが、
当然ポインタを使って void *data; のように本来は持つべきもの
である。ちなみに、最初に root に NULL を入れておくと良いであろう
(最初は要素はないのであるから)。
バイナリーツリーの要素は、例えば次のようにして生成する。
Btree *newCell( int point ){
Btree *bp;
bp = (Btree *)malloc(sizeof(Btree));
bp->point = point;
bp->left = NULL;
bp->right = NULL;
return bp;
}
|
こうして生成した要素をツリーに追加するには、以下のような手順になる。
こうして作成したバイナリーツリーは例えば検索に利用する事が出来る。 検索手順は、与えられた値と現在のポインタの指す要素に格納されている 値とを比較し、小さければ左に進み、大きければ右に進む。勿論、同じ 値があればそこで検索は終了するし、進むべき先がなければ該当する値 は存在しない事になる。
/* Tree に 値newがあれば 1 を返し、なければ 0 を返す */
int search( int new ){
Btree *bp=root;
while(1){
if(bp==NULL){
return 0;
}
if(bp->point == new){
return 1;
}else if(bp->point < new){
bp = bp->left;
}else{
bp = bp->right;
}
}
}
|
バイナリーツリーはうまく扇型に広がっていれば確かに検索にも 効率が良いのだが、扇型に広がるかどうかは単純に登録すると定か ではない。つまりは、入力されるデータの並び順によると言っても良い。 こうした問題を解決する方法が提案されているが、ここでは取り上げない。 また、バイナリーツリーに登録したデータを別の観点で検索するには、 結局全ての要素を検索する必要があり、その場合の検索方法には少し 工夫が必要であるが、これも興味があれば自分で調べて欲しい。