6.3 課題6

cd c を実行した後で（ ~/c に移動した後で）、以下の課題を やってみよ。

課題 6.1
出題プログラムを動かしてみる
以下のプログラムを実行し、正解が得られるまで試みよ。 
/* kadai 6.1 */
#include <stdio.h>
main()
{
        int a, b, c, ans, mondaisu, seikaisu;
        char buf[64];
        mondaisu = 4;
        seikaisu = 0;

        printf("以下の問題では、真の時は１を、偽の時は０を入力せよ。\n\n");

        /* prob. 1 */
        a=5; b=3;
        printf("a=%d, b=%d の時、a>1 && b>2 は真(1)か偽(0)か? 答=> ",a,b);
        scanf("%d",&ans);
        if ( ans == (a>1 && b>2) ){
                seikaisu++;
        }
        scanf("%s",buf);

        /* prob. 2 */
        a=2; b=-2;
        printf("\na=%d, b=%d の時、a<0 || b<0 は真(1)か偽(0)か? 答=> ",a,b);
        scanf("%d",&ans);
        if ( ans == (a<0 || b<0) ){
                seikaisu++;
        }
        scanf("%s",buf);

        /* prob. 3 */
        a=-4; b=-2;
        printf("\na=%d, b=%d の時、a<0 && !b>0 は真(1)か偽(0)か? 答=> ",a,b);
        scanf("%d",&ans);
        if ( ans == (a<0 && !b>0) ){
                seikaisu ++;
        }
        scanf("%s",buf);

        /* prob. 4 */
        a=8; b=-2; c=0;
        printf("\na=%d, b=%d, c=%d の時、",a,b,c);
        printf("a>0 && b>-2 || c>-1 は真(1)か偽(0)か? 答=>");
        scanf("%d",&ans);
        if ( ans == (a>0 && b>-2 || c>-1) ){
                seikaisu ++;
        }
        scanf("%s",buf);

        printf("正解は、%d 問中 %d 問です。\n", mondaisu, seikaisu);
        if (mondaisu == seikaisu){
                printf("全問正解です。次の課題に進んで下さい。\n");
        }else{
                printf("もう一度やり直してください。\n");
        }
}

このプログラムでは、入力された答と論理式の真偽が一致しているかどうかを調べる 為に、if 文の条件式に ans == 論理式 で判定している。

課題 6.2
三角形の成立条件

三角形の３辺の長さを与えたときに、その三角形が成立しているかどうかを 調べるプログラムを作る。注意すべきは、どんな長さの３辺を与えても三角形が 成立するわけではない点である。例えば、斜辺の長さが異常に長い 1000 のような 値をとるときに、他の２辺が 1,1 の長さならば明らかに、これは三角形として 成立しない。一般に三角形の三辺を a, b, c とすると、一般に三角形の成立条件は、 $ a + b > c$ かつ $ b + c > a $ かつ $ c + a > b $ である。

３辺の長さ（自然数）をキーボードから入力して、三角形として成立するかどうか を判定するプログラムを作れ。

課題 6.3
三角形の形状

課題 6.2 のプログラムを利用して、三角形の成立条件を調べた上で、形状を調べる プログラムを作ろう。三角形の形状には色々なものがあるが、ここでは直角三角形 、鈍角三角形、鋭角三角形のどれであるかを調べるプログラムを作る。以下では、 もっとも長い辺を a とし、それ以外の辺を b, c とする。(但し、どれか２つ、 あるいは３つの辺が等しい場合も含む。)

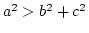  1. 直角三角形 $a^2 = b^2 + c^2$ が成立するもの
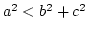  2. 鈍角三角形 $a^2 > b^2 + c^2$ が成立するもの
  3. 鋭角三角形 $a^2 < b^2 + c^2$ が成立するもの

ヒント もっとも長い辺（斜辺）を求めるには次のようにする。 

        int a, b, c, temp;
	...
	if (a < b){
             temp=a; a=b; b=temp;    /* swap a, b */
	}
	if (a < c){
	     temp=a; a=c; c=temp;    /* swap a, c */
	}

これで $ a \ge b, a \ge c $ になっている。

色々な三角形について、作成したプログラムを走らせてみよ。特に、5,4,3 の 三角形、3,2,6 の三角形、5,4,6 の三角形についての結果を報告せよ。

作成したプログラムと結果をメイルで、creport まで送ること。但し、題は kadai06 と すること。


最初のページ 戻る 目次
Hiroyasu Asami