有限桁の小数を扱う方法を考えて見よう。色々な方法が考えられるが、
非常に単純に整数部分を4桁、小数部分を4桁に分けて、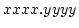 のようにしてみる。すると、
のようにしてみる。すると、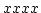 と
と 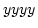 という4桁づつの整数
で表現出来る。例えば、1.123 は、1.1230 と考えて、1 と 1230 の
2つの整数で表現出来る。しかし、この方法では、すぐさま問題が
生じる事が分かる。なぜなら、明らかに1万以上の数が扱えないから
である。このように、小数点の位置を固定してしまうと何かと都合が
悪いので、小数点の位置を固定しない浮動小数点という方法で実数は
表現するようになっている。浮動小数という方法は、簡単に言えば、
整数と10 の指数で表す次のようなものであると思えば良い。
という4桁づつの整数
で表現出来る。例えば、1.123 は、1.1230 と考えて、1 と 1230 の
2つの整数で表現出来る。しかし、この方法では、すぐさま問題が
生じる事が分かる。なぜなら、明らかに1万以上の数が扱えないから
である。このように、小数点の位置を固定してしまうと何かと都合が
悪いので、小数点の位置を固定しない浮動小数点という方法で実数は
表現するようになっている。浮動小数という方法は、簡単に言えば、
整数と10 の指数で表す次のようなものであると思えば良い。
一般には、
と書けるので、整数 a, b を用いて、かなりの範囲の実数を記述する
ことが出来るが、それでも限界があることは良く覚えておかなければ
ならない。(実際にはもう少し複雑な表現方法を用いている。)
最初のページ 戻る 次へ
最後のページ 目次
Hiroyasu Asami